Loading... # 题目描述 设有 $N\times N$ 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字$0$。如下图所示: 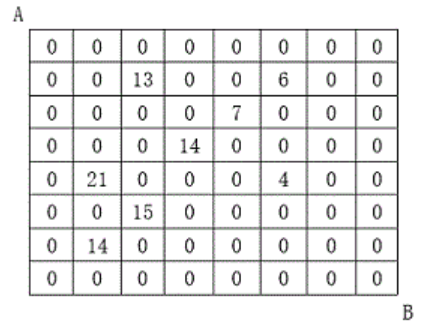 某人从图中的左上角$A$出发,可以向下行走,也可以向右行走,直到到达右下角的$B$点。 在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字$0$)。 此人从$A$点到$B$点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。 # 输入格式 第一行为一个整数$N$,表示$N\times N$ 的方格图。 接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。 行和列编号从$1$开始。 一行“$0 0 0$”表示结束。 # 输出格式 输出一个整数,表示两条路径上取得的最大的和。 # 解题思路 ## 为什么不可以两遍dp **局部最优解不一定是全局最优解** 考虑某个测试用例, 如果两次DP的结果如下: 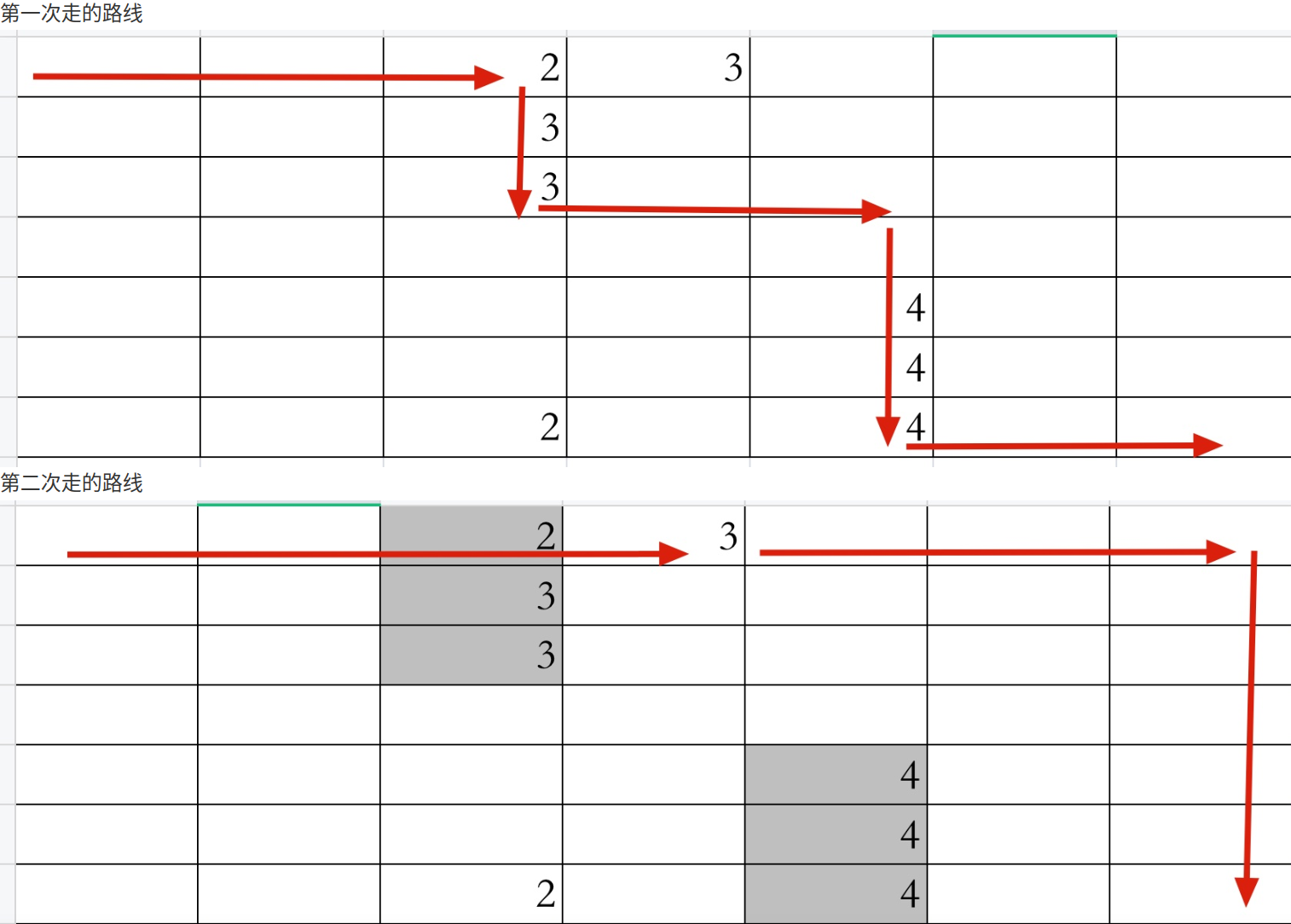 但实际上存在全局最优解如下 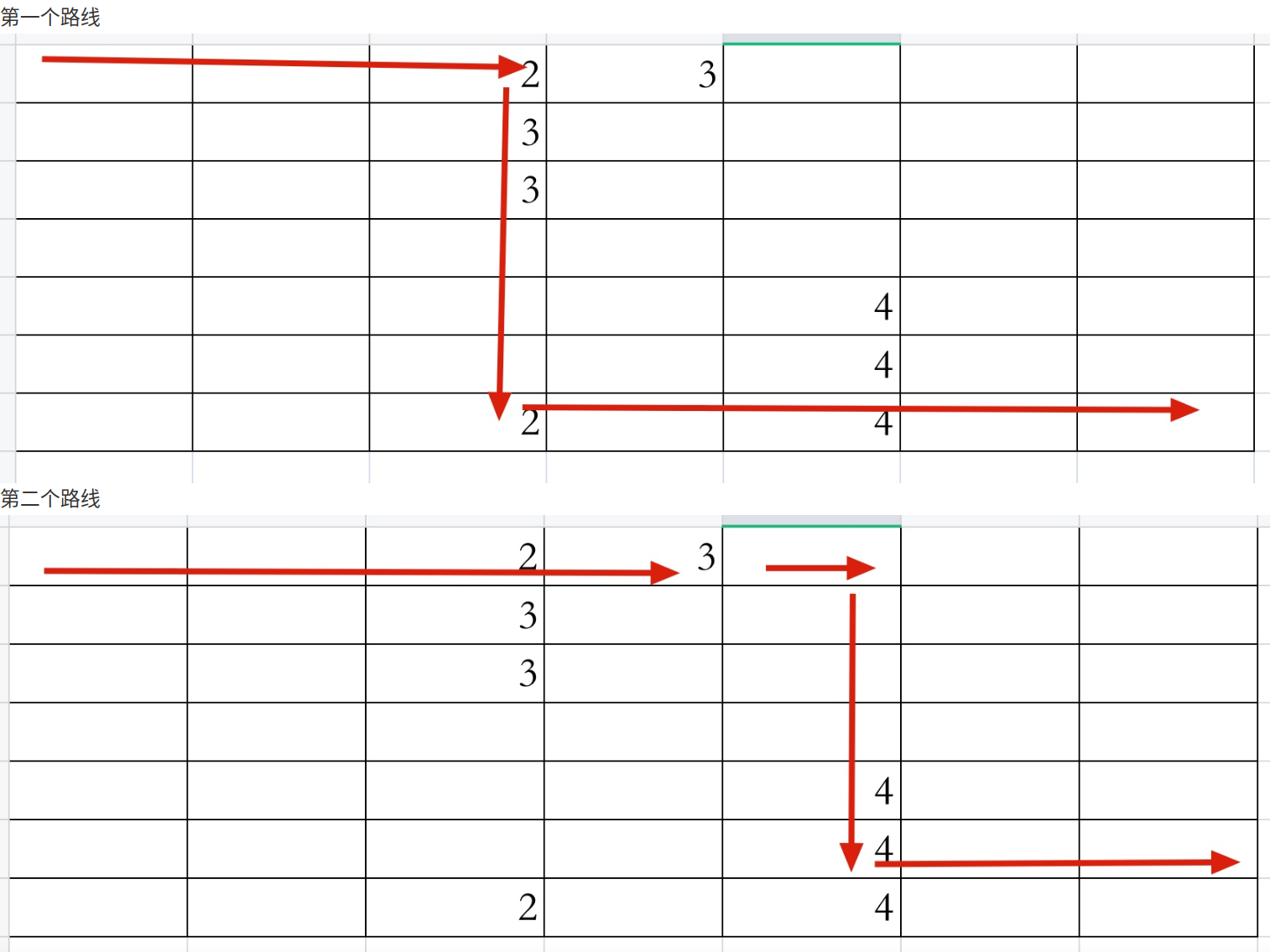 ## 怎么解决这个问题 因此需要考虑如何**在一次DP内解决这个问题**, 朴素的思路如下: 每次dp的过程便利`dp[i1][j1][i2][j2]`,然后 - 对于`i1!=i2||j1!=j2`按照如下方式更新 ```cpp dp[i1][j1][i2][j2]=max( dp[i1 - 1][j1][i2 - 1][j2], dp[i1 - 1][j1][i2 - 1][j2], dp[i1 - 1][j1][i2 - 1][j2], dp[i1 - 1][j1][i2 - 1][j2] )+a[i1][j1]+a[i2][j2] ``` - 对于`i1==i2&&j1==j2`,按照如下方式更新 ```cpp dp[i1][j1][i2][j2]=max( dp[i1 - 1][j1][i2 - 1][j2], dp[i1 - 1][j1][i2 - 1][j2], dp[i1 - 1][j1][i2 - 1][j2], dp[i1 - 1][j1][i2 - 1][j2] )+a[i1][j1] ``` ``` ``` 但这样子的想法还是有一些错误, 因为没有考虑到问题的限制条件: - 在本问题中, 考虑两次遍历一起进行, 因此应该有`i1+j1=i2+j2=k` - 因此,直接进行如上所示的四维dp是不合理的, 同时考虑到这个限制条件也可以将dp降维到三维 ## 解决方案 按照dp问题的分析方式有 - 状态表示 - 集合:`dp[k][i1][i2]`表示所有第一次遍历横坐标为`l1`,纵坐标为`k-l1`; 第二次遍历横坐标为`l2`, 纵坐标为`k-l2`的路线 - 属性:所有路线当中取得的数字的总和最大的 - 状态计算 - 如果`i1==i2`, 则说明遍历到同一个点, 只可以取一次 ```cpp int tmp = a[i1][k - i1]; if(i1 != i2) tmp += a[i2][k - i2]; ``` - 1从左侧更新, 2从左侧更新 ```cpp int t = dp[k - 1][i1 - 1][i2 - 1]; ans = max(ans, t); ``` - 1从左侧更新, 2从上侧更新 ```cpp t = dp[k - 1][i1 - 1][i2]; ans = max(ans, t); ``` - 1从上侧更新, 2从左侧更新 ```cpp t = dp[k - 1][i1][i2 - 1]; ans = max(ans, t); ``` - 1从上侧更新, 2从上侧更新 ```cpp t = dp[k - 1][i1][i2]; ans = max(ans, t); ``` # AC代码 ```cpp #include <cstdio> #include <cstdlib> #include <iostream> #include <vector> #include <cstring> #define endl '\n' using namespace std; const int N = 20; int dp[N][N][N]; int a[N][N]; int n; int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin >> n; while(1) { int x, y, c; cin >> x >> y >> c; if(x == 0 && y == 0 && c == 0) break; a[x][y] = c; } for(int k = 2; k <= 2 * n; k ++) { for(int i1 = 1; i1 < k; i1 ++) { int j1 = k - i1; for(int i2 = 1; i2 < k; i2 ++) { int j2 = k - i2; int ans = 0; int tmp = a[i1][k - i1]; if(i1 != i2) tmp += a[i2][k - i2]; //1从左, 2从左 int t = dp[k - 1][i1 - 1][i2 - 1]; ans = max(ans, t); //1从左, 2从上 t = dp[k - 1][i1 - 1][i2]; ans = max(ans, t); //1从上, 2从左 t = dp[k - 1][i1][i2 - 1]; ans = max(ans, t); //1从上, 2从上 t = dp[k - 1][i1][i2]; ans = max(ans, t); dp[k][i1][i2] = ans + tmp; } } } cout << dp[2 * n][n][n] << endl; return 0; } ``` 最后修改:2025 年 03 月 07 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏