Loading... # 最大似然为什么对应最小距离 ## 条件概率 对于$y=x+w$, 其中$w\sim N(a, M_1)$ 由于在任意给定$x$的情况下, $y$的取值是$w$的概率分布函数, 因此有 $$ \begin{aligned} P(y|x) &=P(w)\\ &=\frac{1}{2\pi \sqrt{M_1}}e^{-\frac{1}{2}\frac{(x - a)^2}{M_1}} \end{aligned} $$ ## 联合概率分布 对于$x_1\sim N(\mu_1, \sigma^2_1), x_2 \sim N(\mu_2, \sigma^2_2)$, 且$x_1, x_2$相互独立, 有 $$ \begin{aligned} P(x_1, x_2) &=P(x_1)P(x_2) \\ &=\frac{1}{2\pi \sqrt{\sigma^2_1}}e^{-\frac{1}{2}\frac{(x_1 - \mu_1)^2}{\sigma^2_1}} \frac{1}{2\pi \sqrt{\sigma^2_2}}e^{-\frac{1}{2}\frac{(x_2 - \mu_2^2)}{\sigma^2_2}} \\ &=\frac{1}{2\pi \sqrt{\sigma^2_1 \sigma^2_2}}e^{-\frac{1}{2}\{\frac{(x_1 - \mu_1)^2}{\sigma^2_1} + \frac{(x_2 - \mu_2)^2}{\sigma^2_2}\}} \end{aligned} $$ 令$\boldsymbol{x}=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$, 不难看出可以对$\frac{(x_1 - \mu_1)^2}{\sigma^2_1} + \frac{(x_2 - \mu_2^2)}{\sigma^2_2}$作如下等价变形: - 令$\boldsymbol{\mu} = \left(\begin{array}{c}\mu_1\\\mu_2\end{array}\right)$, 则$\boldsymbol{x - \mu} = \left(\begin{array}{c}x_1 - \mu_1\\ x_2 - \mu_2\end{array}\right)$ - 令$\boldsymbol{\Sigma}=\left(\begin{array}{cc}\sigma^2_1 & 0\\ 0 & \sigma^2_2 \end{array}\right)$, $\boldsymbol{\Sigma^{-1}}=\left(\begin{array}{cc}\frac{1}{\sigma^2_1} & 0\\ 0 & \frac{1}{\sigma^2_2} \end{array}\right)$ - 令$\boldsymbol{y} = \boldsymbol{(x - \mu)^T\Sigma^{-1}(x - \mu)}$, 则有$\boldsymbol{y} = \frac{(x_1 - \mu_1)^2}{\sigma^2_1} + \frac{(x_2 - \mu_2)^2}{\sigma^2_2}$ 因此有 $$ \begin{aligned} P(x_1, x_2) &=P(x_1)P(x_2) \\ &=\frac{1}{2\pi \sqrt{|\boldsymbol{\Sigma}|}}e^{-\frac{1}{2}\{\boldsymbol{(x - \mu)^T\Sigma^{-1}(x - \mu)}\}} \\ \end{aligned} $$ ## 最大似然和最小距离 假设$y_1 = x_1 + w_1$, $y_2 = x_2 + w_2$, $w_1$, $w_2$相互独立, $w_1 \sim N(a, M_1)$, $w_2\sim N(b, M_2)$, 令$\boldsymbol{x}=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$, $\boldsymbol{y}=\left(\begin{array}{c}y_1\\y_2\end{array}\right)$ 给定$x_1, x_2$的情况下, $y_1, y_2$的取值是$w_1, w_2$的概率函数, 又因为$w_1, w_2$相互独立 由联合概率分布可得, 似然函数$P(\boldsymbol{y}|\boldsymbol{x})$的推导如下: $$ \begin{aligned} P(\boldsymbol{y}|\boldsymbol{x}) &=P(w_1)P(w_2)\\ &=\frac{1}{2\pi \sqrt{M_1 M_2}}e^{-\frac{1}{2}\{\frac{(w_1 - a)^2}{M_1} + \frac{(w_2 - b)^2}{M_2}\}} \\ &=\frac{1}{2\pi \sqrt{|\boldsymbol{\Sigma}|}}e^{-\frac{1}{2}\{\boldsymbol{(x - \mu)^T\Sigma^{-1}(x - \mu)}\}} \\ \end{aligned} $$ 其中, $\boldsymbol{x}=\left(\begin{array}{c}x_1\\x_2\end{array}\right)$, $\boldsymbol{\mu} = \left(\begin{array}{c}a \\ b\end{array}\right)$, $\boldsymbol{\Sigma}=\left(\begin{array}{cc}M_1 & 0\\ 0 & M_2\end{array}\right)$ ### 最大化似然函数就是最小化距离证明 首先, 先明确最小化距离是最小化谁和谁的最小距离: 这里最小化最小距离是指**最小化观测数据$y$与真实信号$x$之间的距离** 对上面的公式作等价变形有 $$ \begin{aligned} P(\boldsymbol{y}|\boldsymbol{x}) &=P(w_1)P(w_2)\\ &=\frac{1}{2\pi \sqrt{M_1 M_2}}e^{-\frac{1}{2}\{\frac{(w_1 - a)^2}{M_1} + \frac{(w_2 - b)^2}{M_2}\}} \\ &=\frac{1}{2\pi \sqrt{M_1 M_2}}e^{-\frac{1}{2}\{\frac{(y_1 - x_1 - a)^2}{M_1} + \frac{(y_2 - x_2 - b)^2}{M_2}\}} \\ \end{aligned} $$ 最大化$P(\boldsymbol{y}|\boldsymbol{x})$等价于最大化对数似然函数$\boldsymbol{L(y)} = ln(P(\boldsymbol{y}|\boldsymbol{x}))$, 相当于最小化$\frac{(y_1 - x_1 - a)^2}{M_1} + \frac{(y_2 - x_2 - b)^2}{M_2}$ 现在设有两个二次函数$z_1 = x_1 + a$, $z_2 = x_2 + b$, 有对于给定的$x_1, x_2$情况下预测得到的$y_1(A)$,$y_2(B)$, 实际为$z_1(A), z_2(B)$ 为了让预测尽可能的准确, 可以采用的方式是最小化$\alpha_1(y_1 - z_1)^2 + \alpha_2(y_2 - z_2)^2$, 其中$\alpha_1, \alpha_2$为调整权重 因此, 最小化$\frac{(y_1 - x_1 - a)^2}{M_1} + \frac{(y_2 - x_2 - b)^2}{M_2}$的几何意义为最小化预测值$A, B$和实际值$C, D$之间的距离$\alpha_1 AB+\alpha_2CD$ 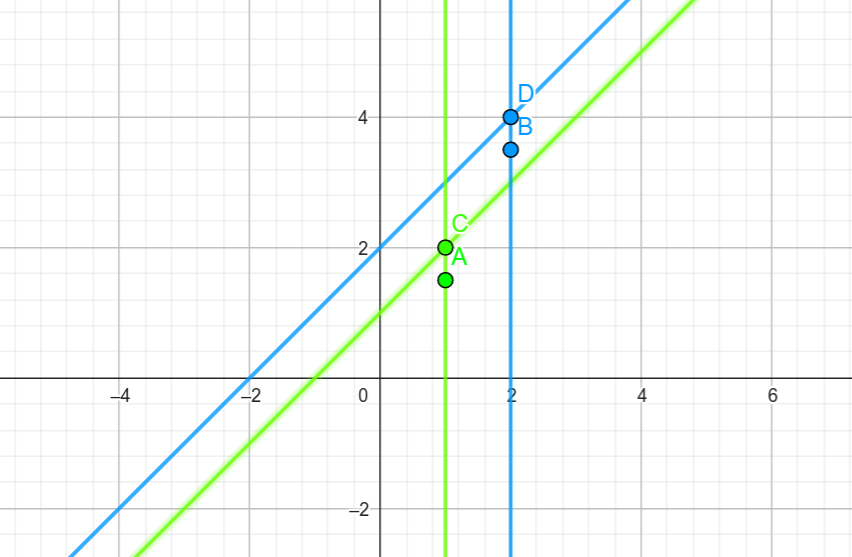 最后修改:2025 年 03 月 07 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏