Loading... # 题目描述 有$N$种物品和一个容量是$V$的背包。 第$i$种物品最多有$s_i$件,每件体积是$v_i,价值是$w_i$。 求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。 # 输入 第一行两个整数$N,V(0< N \leq 1000, 0< V \leq 20000)$ ,用空格隔开,分别表示物品种数和背包容积。 接下来有$N$行,每行三个整数$v_i,w_i,s_i$,用空格隔开,分别表示第$i$种物品的体积、价值和数量。 # 输出 输出一个整数,表示最大价值。 # 数据范围 $0<N\le 1000, 0<V\le 20000, 0<v_i,w_i,s_i\le 20000$ # 解题思路 在数据量过大的情况下, 原始的暴力循环已经不可取, 此时需要寻找一个更快的优化方式作为替代 考虑原始的多重背包问题的分析: - 状态表示: - 集合:`dp[i][j]`表示前`i`个物品, 总体积为`j`的选择方式的集合 - 属性:所有选择方式中价值的最大值 - 状态计算 - 不选择第`i`个物品:`dp[i][j] = max(dp[i][j], dp[i - 1][j])` - 选择第`i`个物品:`dp[i][j] = max(dp[i][j], dp[i - 1][j - v] + w, dp[i - 1][j - 2v] + 2w, ..., dp[i - 1][j - sv] + sw)` - 综合可得:`dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v] + w, dp[i - 1][j - 2v] + 2w, ..., dp[i - 1][j - sv] + sw)` 为了优化这个问题, 需要利用之前计算得到的信息, 假设$r = j % v$,$r \in [0, v)$,对如下的递推公式进行分析 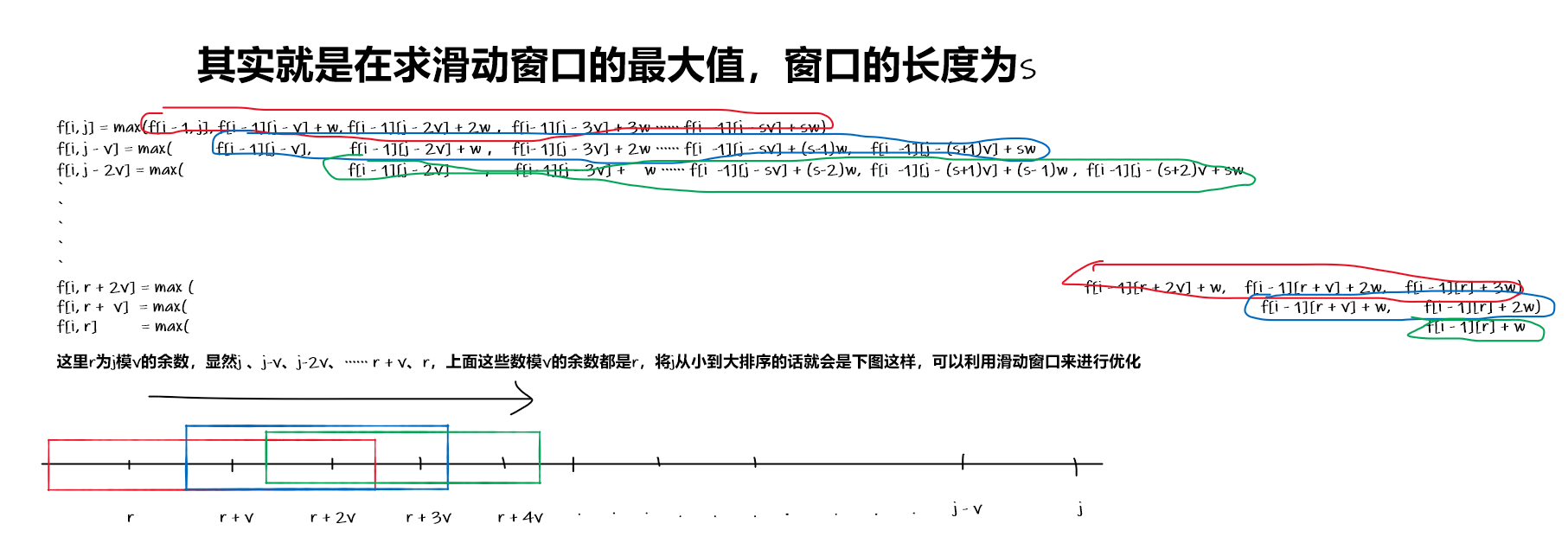 不难看出这个过程实际上是在更新`dp[i][r + kv]`为这样子的滑动窗口中元素的最大值: - 滑动窗口的最后一个元素是`dp[i - 1][r + kv]` - 整个滑动窗口的长度$L \le s_i$ 因此可以使用单调队列对上述过程过程进行优化 具体优化思路如下: ``` 循环 i: 从小到大遍历每一种物品 循环 r: 遍历所有的余数[0, v_i) 双端队列deque, 用于存储单调队列中对于第i中物品拿走的重量 循环 k: 从小到大遍历所有拿走的物品的可能性 判断当前队头元素是否已经划出滑动窗口并处理 利用队头元素更新状态dp[i][k] 利用单调队列的规则将新元素入队 ``` 其中, 还需要处理的是如何比较队伍中元素的大小和利用队头元素更新状态 - 单调队列中存储的是当前物品`i`拿走的重量 - 比较元素的大小是在比较当前元素`dp[i][k]`和上一个物品中的最大值`dp[i - 1][q.front()] + (k - q.front()) / v * w`之间的大小关系 - 其中`(k - q.front()) / v * w`是在计算对于当前的`k`来说应该增加的最大价值是多少 # AC代码 ```cpp #include <cstdio> #include <cstdlib> #include <iostream> #include <vector> #include <cstring> #include <deque> #define endl '\n' using namespace std; const int N = 1e3 + 10; int n, m; int dp[N]; int rec[N]; int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin >> n >> m; for(int i = 1; i <= n; i ++) { int v, w, s; cin >> v >> w >> s; memcpy(rec, dp, sizeof dp); for(int r = 0; r < v; r ++) { deque<int> q; for(int k = r; k <= m; k += v) { if(q.size() && q.front() < k - s * v) q.pop_front(); if(q.size()) dp[k] = max(dp[k], rec[q.front()] + (k - q.front()) / v * w); while(q.size() && rec[q.back()] + (k - q.back()) / v * w < rec[k]) q.pop_back(); q.push_back(k); } } } cout << dp[m] << endl; return 0; } ``` 最后修改:2025 年 03 月 07 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏