Loading... # 题目描述 有$N$个物品和一个容量是$V$的背包。 物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。 如下图所示: 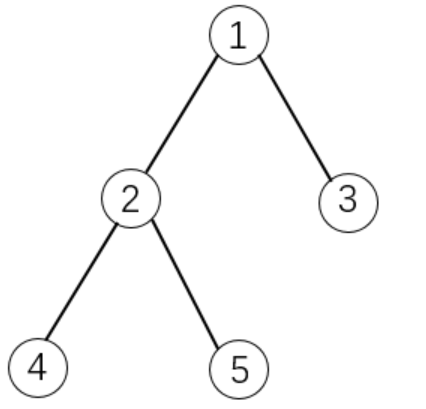 如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。 每件物品的编号是$i$,体积是$v_i$,价值是$w_i$,依赖的父节点编号是$p_i$。物品的下标范围是$1...N$。 求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。 输出最大价值。 # 输入格式 第一行有两个整数$N,V$,用空格隔开,分别表示物品个数和背包容量。 接下来有$N$行数据,每行数据表示一个物品。 第$i$行有三个整数$v_i, w_i, p_i$用空格隔开,分别表示物品的体积、价值和依赖的物品编号。 如果$p_i$ = 1,表示根节点。 **数据保证所有物品构成一棵树。** # 输出格式 输出一个整数,表示最大价值。 # 数据范围 $1\leq N,V\leq 100$ $1\leq v_i,w_i\leq 100$ # 解题思路 对于一般的背包问题, 第`i`个节点的状态只和第`i - 1`个节点的状态有关 而对于这个背包问题, 由于物品间的依赖关系成树形结构, 第`i`个节点的状态可以和任意一个节点都有关系, 根据任意一个节点选或不选, 可以有$2^N$个状态转换, 因此会超时 所以考虑采用不同的决策方案, 放弃原有的按照状态来划分的决策方案, 而采用按照体积来划分的决策方案, 此时无论第`i`个节点是由那些状态转移得到, 对应的体积最多有$V + 1$个, 时间符合要求 按照以上思路进行状态分析, 对于每一个的状态分析仅考虑当前子树的根和其儿子节点(只有一层的子树), 有: - 状态表示: - 集合:`dp[i][u][j]`:以物品`i`为根的树中由第`u`颗子树转移得到的, 总重量不超过`j`的状态 - 属性:最大值 - 状态计算: - 初始化:`dp[i][0][j] = w[i]` - 选择第`u`颗子树:`dp[i][u][j] = max(dp[i][u][j], dp[i][u - 1][j - k] + dp[u][u的最后一个儿子节点][k])` - 不选择第`u`颗子树:`dp[i][u][j] = dp[i][u - 1][j]` 还可以对上述代码进行滚动数组优化, 只需要倒序便利重量`j`即可 # AC代码 ```cpp #include <cstdio> #include <cstdlib> #include <iostream> #include <vector> #include <cstring> #define endl '\n' using namespace std; const int N = 110; int n, m; int dp[N][N]; int h[N], e[N], ne[N], idx; int root; int ans = 0; int v[N], w[N]; void add(int a, int b) { e[idx] = b; ne[idx] = h[a]; h[a] = idx ++; } void dfs(int x) { for(int i = v[x]; i <= m; i ++) dp[x][i] = w[x]; for(int i = h[x]; i != -1; i = ne[i]) { int t = e[i]; dfs(t); for(int j = m; j >= v[x]; j --) { for(int k = 0; k <= j - v[x]; k ++) { dp[x][j] = max(dp[x][j], dp[x][j - k] + dp[t][k]); } } } } int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); memset(h, -1, sizeof h); cin >> n >> m; for(int i = 1; i <= n; i ++) { int p; cin >> v[i] >> w[i] >> p; if(p == -1) root = i; else { add(p, i); } } dfs(root); cout << dp[root][m] << endl; return 0; } ``` 最后修改:2025 年 03 月 07 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏