Loading... # ACWing 340 通信线路 题解 ## 题目描述 多年以后,笨笨长大了,成为了电话线布置师。由于地震使得某市的电话线全部损坏,笨笨是负责接到震中市的负责人。该市周围分布着 $1\le N\le1000$ 根据 $1\cdots N$ 顺序编号的废弃的电话线杆,任意两根线杆之间没有电话线连接,一共有 $1\le p\le10000$ 对电话杆可以拉电话线。其他的由于地震使得无法连接。 第i对电线杆的两个端点分别是 $a_i$ ,$b_i$,它们的距离为 $1\le l_i\le1000000$。数据中每对 $(a_i,b_i)$ 只出现一次。编号为 $1$ 的电话杆已经接入了全国的电话网络,整个市的电话线全都连到了编号 $N$ 的电话线杆上。也就是说,笨笨的任务仅仅是找一条将 $1$ 号和 $N$ 号电线杆连起来的路径,其余的电话杆并不一定要连入电话网络。 电信公司决定支援灾区免费为此市连接 $k$ 对由笨笨指定的电话线杆,对于此外的那些电话线,需要为它们付费,总费用决定于其中最长的电话线的长度(每根电话线仅连接一对电话线杆)。如果需要连接的电话线杆不超过 $k$ 对,那么支出为 $0$。 请你计算一下,将电话线引导震中市最少需要在电话线上花多少钱? ## 输入 输入文件的第一行包含三个数字 $n,p,k$。 第二行到第 $p+1$ 行,每行分别都为三个整数 $a_i,b_i,l_i$。 ## 输出 一个整数,表示该项工程的最小支出,如果不可能完成则输出 `-1`。 ## 解题思路 ### 分层图 由题意可知, 最多允许$k$条边的权重为$0$, 因此可以考虑建立$k + 1$层图, 设$a_{ij}$表示第$i$层图标号为$j$的节点, 其中假设节点$a_{1i}$和节点$a_{1j}$之间有一条权重为$w$的边, 则对于$\forall t \in [1, k]$, 都可以有$a_{ti}$到$a_{tj}$的边, 其权重为$0$。 当$k = 1$时, 只需要建立两层图即可,此时的图如下图所示 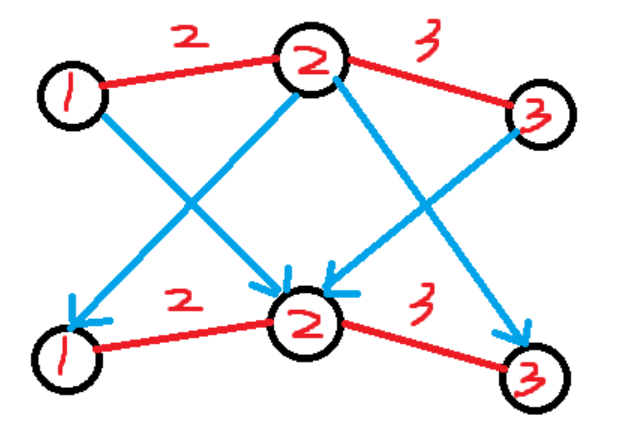 不难发现, 有$k$条边的边权变为$0$的情况下的最短路应为从$a_{11}$到$a_{(k+1)3}$的最短路距离 此外, 为了避免还没有到第$k + 1$层图就已经在$a_{jn}, j < k + 1$取到最小值, 导致$a_{(k + 1)n}=INF$, 可以在每一层的终点向下建立一条边权为$0$的有向边 ```cpp #include <cstdio> #include <cstdlib> #include <iostream> #include <vector> #include <cstring> #include <queue> #define endl '\n' using namespace std; const int N = 1e6 + 10, M = 2e7 + 10; typedef pair<int, int> PII; int n, m, k; int h[N], e[M], ne[M], w[N], idx; int dist[N]; bool st[N]; void add(int a, int b, int c) { e[idx] = b; ne[idx] = h[a]; w[idx] = c; h[a] = idx ++; } void dijstra() { memset(st, 0, sizeof st); memset(dist, 0x3f, sizeof dist); priority_queue<PII, vector<PII>, greater<PII>> heap; dist[1] = 0; heap.push({0, 1}); while(heap.size()) { auto t = heap.top(); int d = t.first, u = t.second; heap.pop(); if(st[u]) continue; st[u] = true; for(int i = h[u]; i != -1; i = ne[i]) { int j = e[i], weight = max(dist[u], w[i]); if(dist[j] > weight) { dist[j] = weight; heap.push({dist[j], j}); } } } } int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); memset(h, -1, sizeof h); cin >> n >> m >> k; for(int i = 1; i <= m; i ++) { int a, b, c; cin >> a >> b >> c; add(a, b, c); add(b, a, c); for(int j = 1; j <= k; j ++) { add(a + (j - 1) * n, b + j * n, 0); add(b + (j - 1) * n, a + j * n, 0); add(a + j * n, b + j * n, c); add(b + j * n, a + j * n, c); } } for(int i = 1; i <= k; i ++) { add(i * n, (i + 1) * n, 0); } dijstra(); if(dist[(k + 1) * n] == 0x3f3f3f3f) cout << -1 << endl; else cout << dist[(k + 1) * n] << endl; return 0; } ``` ### 二分搜索 这道题还可以用二分搜索来解决。 不难注意到, 从起点到终点的最短路中, 长度大于$x$的边的数量一定随着$x$的增大单调递减, 因此可以考虑二分边的长度来求得答案。 首先这道题的关键是定义二分的`check`函数, 如何定义`check`函数得到从起点到终点的最短路中, 长度大于$x$的边的数量。<br>可以将这个问题转化为最短路问题, 将长度大于$x$的边的权重置为$1$, 反之置为$0$,则从起点到终点的最短路则为长度大于$x$的边的数量。 接着需要注意二分的区间的初始化, 对于左端点, 显然应该初始化为0, 当$k == m$时候取到左端点; <br>对于右端点, 如果取边权的最大值$10^6$, 则当取到右端点时, 无法判断此时图是否为连通图(因为当图不连通的时候, `check`的返回值一定大于$k$, 最后二分结果也会是$10^6$), 因此需要取$10^6 + 1$来区分无解情况 然后需要注意二分的边界 - 如果`check(mid) <= k`, 则说明答案应该小于`mid`, 因此应该更新`r=mid` - 反之, 则应该更新`l = mid + 1` 最后可以考虑双端队列优化 - 不难发现, 这个问题中所有的边权不是$0$就是$1$, 因此可以考虑用双端队列进行优化, 求得最短路 - 注意:双端队列是在出队的时候得到最小值。 ```cpp #include <cstdio> #include <cstdlib> #include <iostream> #include <vector> #include <cstring> #include <deque> #define endl '\n' using namespace std; const int N = 2e5 + 10; int n, m, k; int h[N], e[N], ne[N], w[N], idx; int dist[N]; bool st[N]; void add(int a, int b, int c) { e[idx] = b; ne[idx] = h[a]; w[idx] = c; h[a] = idx ++; } int bfs(int x) { memset(dist, 0x3f, sizeof dist); memset(st, 0, sizeof st); dist[1] = 0; deque<int> q; q.push_front(1); while(q.size()) { int t = q.front(); q.pop_front(); if(st[t]) continue; st[t] = true; for(int i = h[t]; i != -1; i = ne[i]) { int j = e[i], weight = w[i]; if(weight > x) weight = 1; else weight = 0; if(dist[j] > dist[t] + weight) { dist[j] = dist[t] + weight; if(weight == 1) q.push_back(j); else q.push_front(j); } } } return dist[n]; } int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); memset(h, -1, sizeof h); cin >> n >> m >> k; for(int i = 1; i <= m; i ++) { int a, b, c; cin >> a >> b >> c; add(a, b, c); add(b, a, c); } int l = 0, r = 1e6 + 1; while(l < r) { int mid = l + r >> 1; if(bfs(mid) <= k) r = mid; else l = mid + 1; } if(l == 1e6 + 1) cout << -1 << endl; else cout << l << endl; return 0; } ``` 最后修改:2025 年 03 月 10 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏