Loading... # 理解最小二乘法的本质 在前两节中, 我们探究了矩阵向量乘法在几何角度的意义, 并且从几何角度探究了线性方程组解的个数和精确解的求法。但是我们经常会碰到线性方程组没有解的情况,这个时候虽然无法得到线性方程组的精确解,但如果能够求得一个合理的近似解也是具有重大实践意义的。 下面将从特殊到一般,从一个简单的线性方程组入手, 给出求近似解的同法。下面是一个简单的线性方程组 $$ \left\{ \begin{align} \begin{array}{c} x_1+x_2&=0\\ 2x_1+x_2&=0\\ x_1+x_2&=2 \end{array} \end{align} \right. \tag{1} $$ 将上述线性方程组写为矩阵向量乘法的形式 $$ \boldsymbol{Ax=b} \tag{2} $$ 求该线性方程组的增广矩阵不难发现, 向量$\boldsymbol{b}$无法用矩阵$\boldsymbol{A}$的两个基向量$\boldsymbol{a_1, a_2}$线性表示, 因此该线性方程组没有精确解。 ## 如何求得近似解(具体案例分析) 如果画出向量$\boldsymbol{b}$和矩阵矩阵$\boldsymbol{A}$的两个基向量$\boldsymbol{a_1, a_2}$所张成的列空间$C(\boldsymbol{A})$的关系, 应该如下图所示: 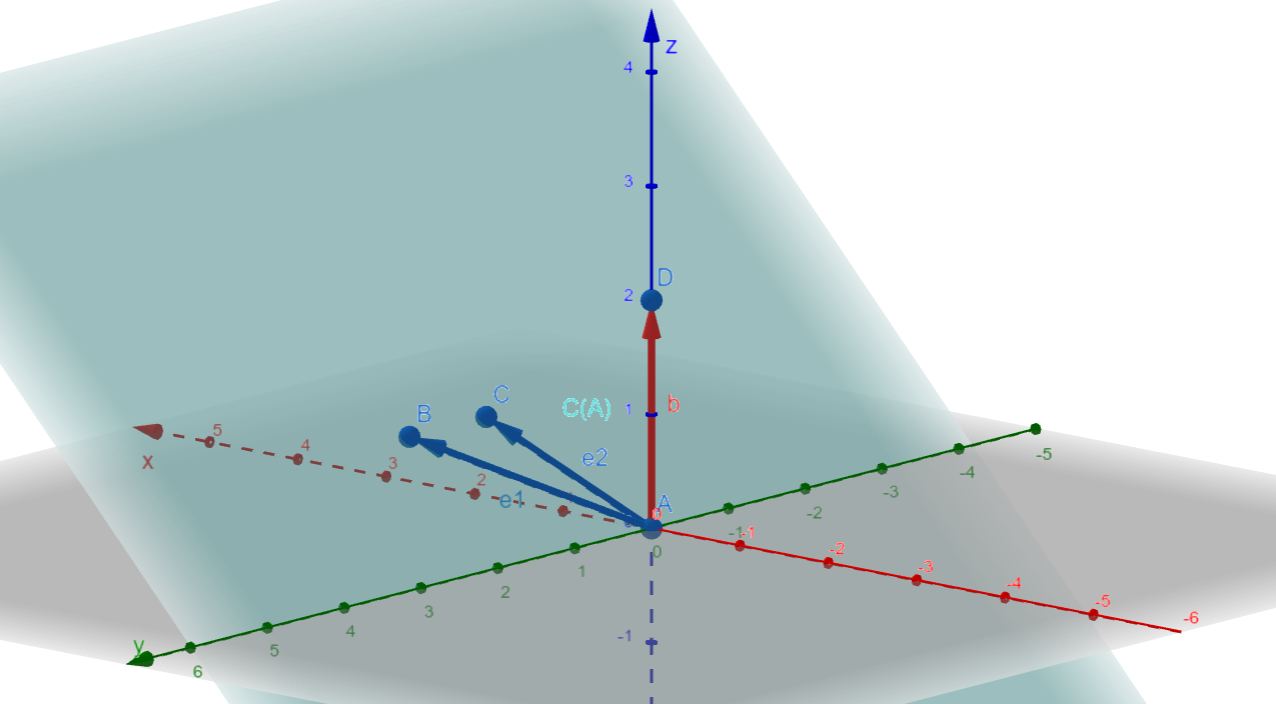 显然是没有精确解的, 因此我们可以考虑求近似解。对于近似解$\boldsymbol{p}$而言, 一定是越近越好,不妨设原向量$\boldsymbol{b}$和近似解$\boldsymbol{p}$之间的误差为$\boldsymbol{e = b - p}$, 则求最相近的解$\boldsymbol{p}$ 等价于求最小的$\boldsymbol{e}$, 由点到直线的距离可知, 将向量$\boldsymbol{b}$向列空间$C(\boldsymbol{A})$投影得到的向量$\boldsymbol{p}$即是最接近的向量。 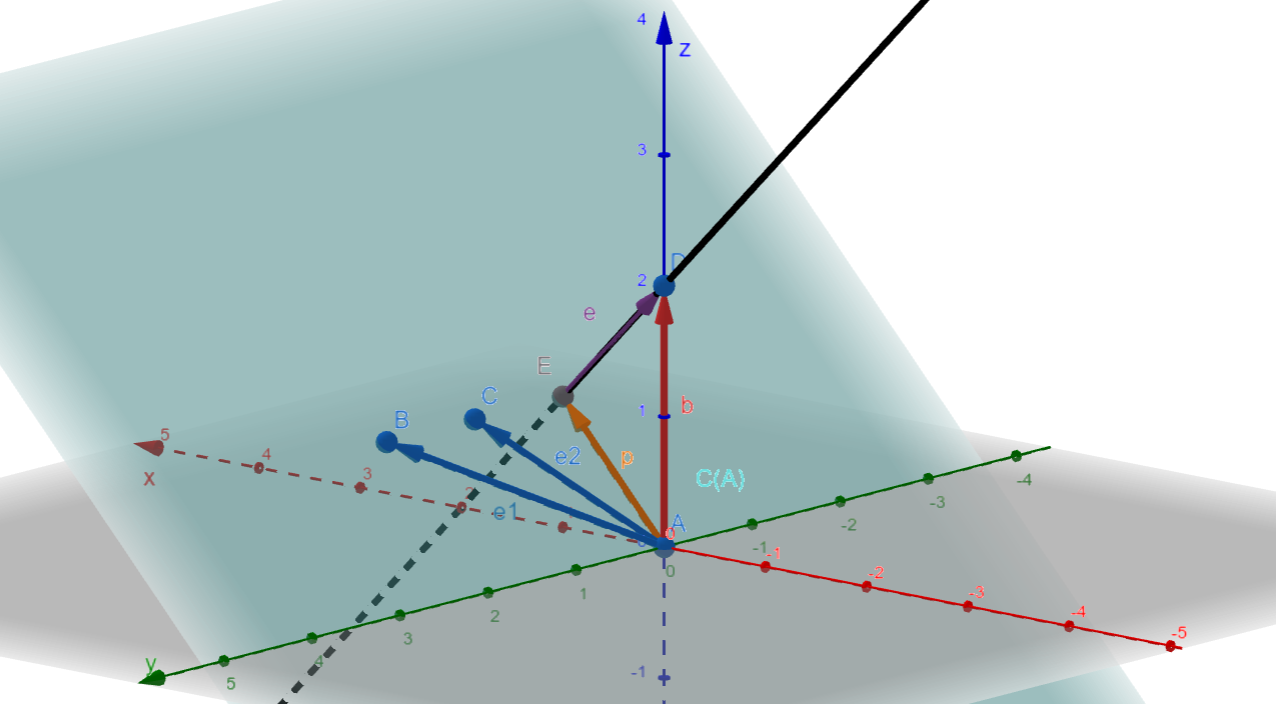 由几何关系不难得出以下几个方程: $$ \left\{ \begin{array}{c} \begin{align} \boldsymbol{b - p}&= \boldsymbol{e} \tag{3}\\ \boldsymbol{e\cdot a_1}&= 0 \tag{4}\\ \boldsymbol{e\cdot a_2}&= 0 \tag{5}\\ \boldsymbol{A}\hat{\boldsymbol{x}} &= \boldsymbol{p}\tag{6}\\ \boldsymbol{Pb}&= \boldsymbol{p} \tag{7}\\ \end{align} \end{array} \right. $$ 其中, $\hat{\boldsymbol{x}}$即为近似解, $\boldsymbol{P}$为将向量$\boldsymbol{b}$变换到向量$\boldsymbol{p}$的变换矩阵 将$(3)$带入$(4)$和$(5)$有 $$ \boldsymbol{a_1\cdot(b-p)}=0\\ \boldsymbol{a_2\cdot(b-p)}=0 $$ 注意到$\boldsymbol{a_1, a_2}$为矩阵$\boldsymbol{A}$的列向量,因此将上式写为矩阵向量乘法的形式 $$ \boldsymbol{a_{1_{1 \times 3}}^{\top}} (\boldsymbol{b - p})_{3\times 1} = 0\\ \boldsymbol{a_{2_{1 \times 3}}^{\top}} (\boldsymbol{b - p})_{3\times 1} = 0 $$ 由$\boldsymbol{A} = \left(\begin{array}{cc}\boldsymbol{a_1} & \boldsymbol{a_2}\end{array}\right)$可以化简上式为 $$ \left( \begin{array}{c} \boldsymbol{a_1^{\top}} \\ \boldsymbol{a_2^{\top}} \end{array} \right)_{2 \times 3} \left( \boldsymbol{b - p} \right) = \boldsymbol{A^{\top}} \left( \boldsymbol{b - p} \right) = \boldsymbol{0} \tag{8} $$ 将$(6)$带入$(8)$, 化简可得 $$ \boldsymbol{A^{\top}A}\hat{\boldsymbol{x}} = \boldsymbol{A^{\top}b} \tag{9} $$ 由于$R(\boldsymbol{A^{\top}A}) = R(\boldsymbol{A})$可知,矩阵$\boldsymbol{A^{\top}A}$存在逆矩阵, 因此有 $$ \hat{\boldsymbol{x}} = \left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}b} \tag{10} $$ 将$(10)$带入$(6),(7)$可得 $$ \hat{\boldsymbol{p}} = \boldsymbol{A}\left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}b} \tag{11} $$ $$ \hat{\boldsymbol{P}} = \boldsymbol{A}\left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}} \tag{12} $$ ### $R(\boldsymbol{A^{\top}A}) = R(\boldsymbol{A})$证明 - $\forall x \in N(\boldsymbol{A})$, 其中$N(\boldsymbol{A})$是$\boldsymbol{A}$的零空间, 对于$\boldsymbol{Ax = 0}$有$\boldsymbol{A^{\top}Ax = 0}$, 因此有$N(\boldsymbol{A^{\top}A})\subseteq N(\boldsymbol{A})$ - 同理, $\forall x \in N(\boldsymbol{A^{\top}A})$, 对于$\boldsymbol{A^{\top}Ax = 0}$有$\boldsymbol{x^{\top}A^{\top}Ax = 0}$即$\boldsymbol{(xA)^{\top}Ax = 0}$, 因此有$\boldsymbol{Ax = 0}$, 故$N(\boldsymbol{A})\subseteq N(\boldsymbol{A^{\top}A})$ - 综上有$N(\boldsymbol{A})=N(\boldsymbol{A^{\top}A})$, 即$n - R(\boldsymbol{A^{\top}A}) = n - R(\boldsymbol{A})$, 即$R(\boldsymbol{A^{\top}A}) = R(\boldsymbol{A})$ ### 施密特正交化的妙用 对于上面推导所得到的公式: $$ \left\{ \begin{array}{c} \hat{\boldsymbol{x}} = \left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}b}\\ \hat{\boldsymbol{p}} = \boldsymbol{A}\left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}b}\\ \hat{\boldsymbol{P}} = \boldsymbol{A}\left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}} \end{array} \right. $$ 有一个显而易见的问题是公式太复杂了, 不便于计算。究其原因则是矩阵$\boldsymbol{A}$的列向量$\boldsymbol{a_i}$是从列空间$C(\boldsymbol{A})$中随意选择的$n$个线性无关的向量作为基向量。 $$ \boldsymbol{A^{\top}A} = \left( \begin{array}{cc} \boldsymbol{a_1^{\top}a_1} & \boldsymbol{a_1^{\top}a_2} \\ \boldsymbol{a_2^{\top}a_1} & \boldsymbol{a_2^{\top}a_2} \\ \end{array} \right) $$ 如果这里进行计算的时候选择$C(\boldsymbol{A})$中的一组特定的基向量, 让他们彼此之间正交$(\boldsymbol{a_i^{\top}a_j} = 0, i \neq j)$, 则此时$\boldsymbol{A^{\top}A}$退化为对角矩阵, 大大的降低计算的复杂程度。 如果再进一步, 让每一个列向量的模长为$1(a_i^{\top}a_i = 1)$, 则此时$\boldsymbol{A^{\top}A}$退化为单位矩阵矩阵 那么如何将得到当前列空间$C(\boldsymbol{A})$所对应的正交基向量呢?对于列向量$\boldsymbol{a_i}$, 如果对于任意的$\boldsymbol{a_j}, j < i$都有$\boldsymbol{a_i^{\top}a_j} = 0$, 则可以保证所有的向量之间相互正交, 在求得一组正交基向量后, 将每一个向量$\boldsymbol{q_i}$除以其模长$|\boldsymbol{q_i}|$, 即可实现单位化。 对于上述的两个列向量来说, 即需要满足如下关系: $$ \begin{align} &\boldsymbol{v_1} = \boldsymbol{a_1}\\ &\boldsymbol{v_2} = \boldsymbol{a_2} - x_1\boldsymbol{a_1}\\ &\boldsymbol{v_1\cdot v_2} = 0 \end{align} \tag{13} $$ 解得 $$ \boldsymbol{v_2} = \boldsymbol{a_2 - \frac{a_1^{\top}a_2}{a_1^{\top}a_1}a_1} \tag{14} $$ 最后在单位化有 $$ q_1 = \frac{v_1}{|v_1|}\\ q_2 = \frac{v_2}{|v_2|} $$ 令$\boldsymbol{Q = \left(\begin{array}{cc}q_1 & q_2\end{array}\right)}$这样, 原方程的解就可以简化为: $$ \left\{ \begin{array}{c} \hat{\boldsymbol{x}} = \boldsymbol{Q^{\top}b} \\ \hat{\boldsymbol{p}} = \boldsymbol{Q}\boldsymbol{Q^{\top}b}\\ \hat{\boldsymbol{P}} = \boldsymbol{Q}\boldsymbol{Q^{\top}} \end{array} \right. \tag{15} $$ 注意, $\boldsymbol{QQ^{\top}}$是一个矩阵而不是常数, 因此可以对向量起到变换的作用。 $$ \begin{align} \boldsymbol{QQ^{\top}} &= \left( \begin{array}{cc} \boldsymbol{q_1} & \boldsymbol{q_2} \end{array} \right) \left( \begin{array}{c} \boldsymbol{q_1^{\top}} \\ \boldsymbol{q_2^{\top}} \end{array} \right)\\ &= \boldsymbol{q_{1_{3 \times 1}}}\boldsymbol{q_{1_{1 \times 3}}^{\top}} + \boldsymbol{q_{2_{3 \times 1}}}\boldsymbol{q_{2_{1 \times 3}}^{\top}} \\ &= \left(\boldsymbol{q_1q_1^{\top} + q_2q_2^{\top}}\right)_{3 \times 3} \end{align} $$ ## 如何求得近似解(一般情况) 对于一般的情况, 为了求得近似解, 则需要解如下的方程组: $$ \left\{ \begin{array}{c} \begin{align} \boldsymbol{b - p}&= \boldsymbol{e} \\ \forall a_i \in A, \boldsymbol{e\cdot a_i}&= 0 \\ \boldsymbol{A}\hat{\boldsymbol{x}} &= \boldsymbol{p}\\ \boldsymbol{Pb}&= \boldsymbol{p} \\ \end{align} \end{array} \right. \tag{16} $$ 方程组$(16)$的解为: $$ \left\{ \begin{array}{c} \hat{\boldsymbol{x}} = \left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}b}\\ \hat{\boldsymbol{p}} = \boldsymbol{A}\left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}b}\\ \hat{\boldsymbol{P}} = \boldsymbol{A}\left(\boldsymbol{A^{\top}A}\right)^{-1}\boldsymbol{A^{\top}} \end{array} \right. $$ 设$n = R(\boldsymbol{A})$为了方便计算, 对于$\forall i \in [1, n]$, 可以循环进行如下的施密特正交化 $$ \boldsymbol{v_i} = \boldsymbol{a_i} - \sum_{j = 1}^{i - 1}x_{ij} \boldsymbol{a_j} \\ \boldsymbol{v_i^{\top} v_j} = 0 (j < i) \tag{17} $$ 方程组$(17)$的解为 $$ x_{ij} = \boldsymbol{\frac{a_j^{\top}a_i}{a_j^{\top}a_j}}, j < i $$ 最后将向量单位化, 即可得到正交矩阵$\boldsymbol{Q} = \left(\begin{array}{cccc}q_1 & q_2 & \cdots & q_n\end{array}\right)$, 满足$\boldsymbol{Q^{\top}Q = I}$ ## 最小二乘法的本质 最小二乘法经常用来处理一条直线近似拟合一群数据点的情况, 我们可以得到如下的判断: - 回顾公式$(1)$, 实际上就是在求解平面上三个点$(1,0)、(2,0)、(1,2)$到直线$y = kx + b$的最小距离 - 求解得到的近似解$\hat{\boldsymbol{x}}$带入公式$(6)$所得到的向量$\boldsymbol{p}$则是近似解对应的纵坐标$\hat{y_i} = k\hat{x_i} + b, \hat{x_i}\in \boldsymbol{\hat{x}}$的集合。 - 在执行最小二乘法的过程中, 最小化$\boldsymbol{e = b - p}$的长度$|\boldsymbol{e}|$相当于最小化近似解对应的纵坐标和原数据点纵坐标的差值的平方$\sum_{i = 1}^{n}(y_i - \hat{y_i})^2$ 因此我们可以得出:**总的来说,传统最小二乘法中“二乘”是平方的意思,“最小二乘”就是指平方和最小,具体来说就是各个测量值和真实值之间的误差的平方和最小化,即各个点横坐标对应的原始点纵坐标与直线上拟合点纵坐标误差的平方和最小化** 最后修改:2025 年 03 月 22 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏