Loading... # 理解相似矩阵对角化 ## 相似矩阵的定义 设$\boldsymbol{A,B}$均为$n$阶方阵, 如果存在可逆矩阵$\boldsymbol{P}$, 满足$\boldsymbol{A = P^{-1}BP}$,则矩阵$\boldsymbol{A, B}$为相似矩阵, 记作$\boldsymbol{A}\sim \boldsymbol{B}$ ## 理解相似矩阵 设在向量空间$\boldsymbol{V_1}$中存在向量$\boldsymbol{v}$(对应线性空间中的$s$点), 对于矩阵$\boldsymbol{A}$, $\boldsymbol{Av}$对应线性空间中的$f$点  如果在向量空间$\boldsymbol{V_2}$中, 点$s$对应的向量为$\boldsymbol{v^{'}}$, 矩阵$\boldsymbol{B}$表示从$s$到$f$的线性变换, 则点$f$对应的向量为$\boldsymbol{Bv^{'}}$ 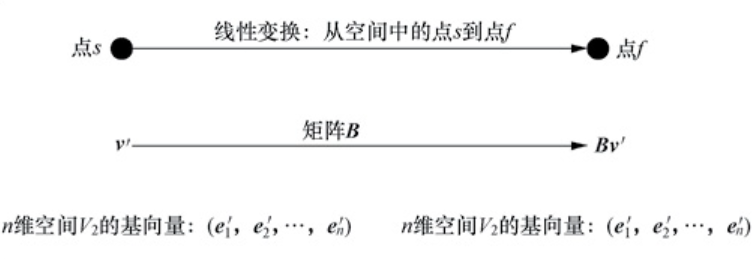 考虑线性空间$\boldsymbol{V_1}$到线性空间$\boldsymbol{V_2}$的映射P, 则应有$\boldsymbol{v^{'} = Pv}$, $\boldsymbol{Bv^{'} = PAv}$, 联立可得, $\boldsymbol{PAv = BPv}$, 即$\boldsymbol{(PA-BP)v=0}$对于任意$\boldsymbol{v}$恒成立, 因此有$\boldsymbol{PA-BP = 0}$, 又有$\boldsymbol{P}$是可逆矩阵有$\boldsymbol{A=P^{-1}BP}$ 因此, $\boldsymbol{A}$和$\boldsymbol{B}$指向了在不同的基底下的相同的线性变换, 因此$\boldsymbol{A}$和$\boldsymbol{B}$为相似矩阵 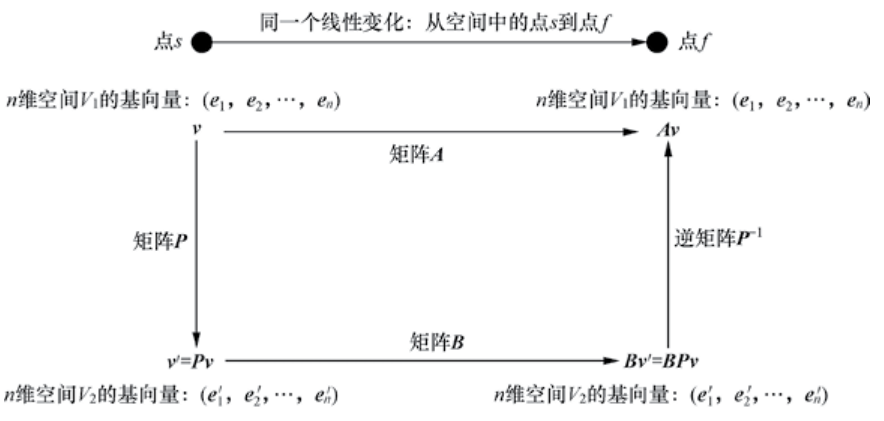 通过上面的分析, 我们可以总结得到相似矩阵的本质: - 相似矩阵**不是**说对于线性空间$\boldsymbol{V}$, 是否存在两个不同的矩阵$\boldsymbol{A, B}$, 他们对于线性空间上的$\boldsymbol{V}$上的变换(平移、伸缩、旋转)是相同的。 - 相似矩阵**是**对于两个不同的线性空间$\boldsymbol{V_1、 V_2}$, 如果矩阵$\boldsymbol{A_1}$对于线性空间$\boldsymbol{V_1}$做线性变换$T_1()$, 矩阵$\boldsymbol{A_2}$对于线性空间$\boldsymbol{V_2}$做线性变换$T_2()$, 如果两个线性变换在各自的线性空间是等效的(即在各自的线性空间发生了相同的平移、伸缩、旋转)。 - 总而言之, 相似矩阵指的是对于两个不同的基底下, 进行同样的线性变换的两个矩阵。 ## 相似矩阵有什么用 在某些情况下, 矩阵$\boldsymbol{A}$比较复杂, 导致计算类似于$\boldsymbol{Av}、A^k$的线性变换较为复杂。而相似矩阵为我们提供了一个全新的思路:如果在基底1$(\boldsymbol{e_1, e_2, \cdots, e_n})$上计算较为复杂, 是否可以通过线性变换$\boldsymbol{P}$先把向量映射到基底2$(\boldsymbol{e_1^{'}, e_2^{'}, \cdots, e_n^{'}})$, 然后在基底2上进行较为简单的线性变换形式(如对角矩阵), 最后在通过$\boldsymbol{P^{-1}}$映射回基底1。 这样, 可以大大简化计算的开销。 ## 如何求得相似矩阵对角化 通过上述分析可知, 为了让相似矩阵发挥其应有的作用, 需要寻找一个基底$(\boldsymbol{e_1^{'}, e_2^{'}, \cdots, e_n^{'}})$, 使得在基底上的线性变换为对角矩阵, 那么应该如何寻找这个对角矩阵$\boldsymbol{\Lambda} = \left(\begin{array}{cccc}\lambda_1 & \cdots & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots& \cdots& \lambda_n\end{array}\right)$呢? 我们知道, 由相似矩阵的性质有$\boldsymbol{\Lambda} = P^{-1}AP$, 将等式的两侧左乘矩阵$\boldsymbol{P}$有$\boldsymbol{P\Lambda} = AP$,将矩阵P写作列向量的形式有 $$ \left( \begin{array}{cccc} \boldsymbol{p_1} & \boldsymbol{p_2} & \cdots & \boldsymbol{p_n} \end{array} \right) \left( \begin{array}{cccc} \lambda_1 & \cdots & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots& \cdots& \lambda_n \end{array} \right) = \boldsymbol{A} \left( \begin{array}{cccc} \boldsymbol{p_1} & \boldsymbol{p_2} & \cdots & \boldsymbol{p_n} \end{array} \right) $$ 化简有 $$ \left( \begin{array}{cccc} \boldsymbol{Ap_1} & \boldsymbol{Ap_2} & \cdots & \boldsymbol{Ap_n} \end{array} \right) = \left( \begin{array}{cccc} \lambda_1\boldsymbol{p_1} & \lambda_2\boldsymbol{p_2} & \cdots & \lambda_n\boldsymbol{p_n} \end{array} \right) $$ 因此有 $$ \left\{ \begin{array}{c} \boldsymbol{Ap_1} = \lambda_1\boldsymbol{p_1} \\ \boldsymbol{Ap_2} = \lambda_2\boldsymbol{p_2} \\ \cdots \\ \boldsymbol{Ap_n} = \lambda_n\boldsymbol{p_n} \\ \end{array} \right. $$ 从上面的推导我们得到$\boldsymbol{Ap_i} = \lambda_i\boldsymbol{p_i}$, 变换一下形式得到$(\boldsymbol{A} - \lambda_i\boldsymbol{I})\boldsymbol{p_i} = \boldsymbol{0}$, 又由$\boldsymbol{p_i}$是矩阵$\boldsymbol{P}$的一个列向量可得, $\boldsymbol{p_i}$一定不为零向量, 由此可以推断出, 矩阵$R(\boldsymbol{A} - \lambda_i\boldsymbol{I}) < n$,变换矩阵将向量$\boldsymbol{p_i}$压缩至零空间, 因此变换后的单位体积为0, 即$det(\boldsymbol{A} - \lambda_i\boldsymbol{I}) = 0$ ## 特征值和特征向量的含义 上述公式$\boldsymbol{Ap_i} = \lambda_i\boldsymbol{p_i}$意味着,一个矩阵和一个向量相乘的效果与一个数和一个向量相乘的效果是相同的。我们知道矩阵$\boldsymbol{A}$与向量$\boldsymbol{p_i}$相乘可以看作对向量$\boldsymbol{p_i}$进行了一次线性变换(旋转、拉伸或压缩),而该变换等效于常数$\lambda_i$乘以向量$\boldsymbol{p_i}$。所以,求解特征向量的过程就是寻找矩阵$\boldsymbol{A}$可以使得哪些向量(特征向量)只发生伸缩变换(而不发生旋转)的过程,具体伸缩变换的程度可以用特征值$\lambda$来表示。 ## 总结 由此我们不难发现为什么选择对角矩阵$\boldsymbol{\Lambda}$作为相似矩阵, 此时可逆矩阵$\boldsymbol{P}$的全部列向量$\boldsymbol{(p_1, p_2, \cdots, p_n)}$恰好组成了一组新的基向量, 而在该基底下, 线性变换$\boldsymbol{A}$被表示为线性变换$\boldsymbol{\Lambda}$, 由于对角矩阵的作用仅仅是对各个坐标分量进行伸缩变换,因此在该基底下, 对于基向量方向的任意向量只发生伸缩变换, 而不发生旋转变换。 最后修改:2025 年 03 月 29 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏